delta star transformer: Electromagnetic Theory, Technical Differences, and Engineering Applications
Introduction
In power system engineering, the delta star connection transformer (Δ–Y transformer) is not merely a conventional wiring choice—it is the result of deep electromagnetic considerations involving magnetic flux balance, zero-sequence current behavior, grounding theory, and harmonic suppression. Compared with other transformer connections (Δ–Δ, Y–Y, Y–Δ), the delta–star configuration demonstrates superior system stability under real-world operating conditions.
This article takes delta star transformer as the core keyword and provides a deeper, formula-based explanation of why this topology dominates modern medium- and low-voltage distribution networks, especially from the perspective of electromagnetic field theory and power system analysis.
Definition of Delta star Connection Transformer
A delta star connection transformer is characterized by:
- Primary winding connected in delta (Δ)
- Secondary winding connected in star (Y or Yn), usually with a grounded neutral
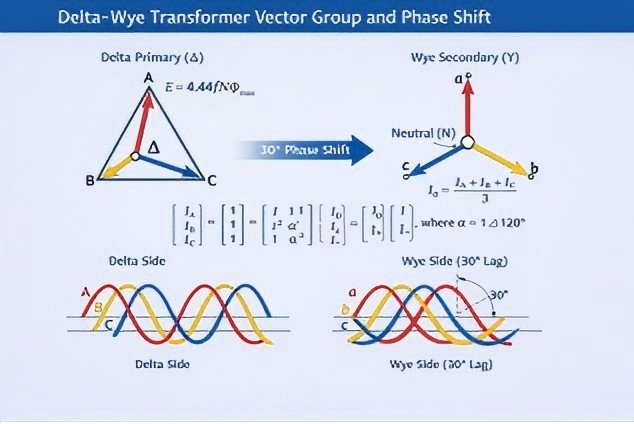
The most common IEC vector groups are Dyn11 and Dyn1, indicating a ±30° phase displacement between primary and secondary line voltages.
Fundamental Electromagnetic Theory
1. Transformer EMF Equation and Flux Relationship
The induced electromotive force (EMF) in a transformer winding is governed by:
E = 4.44 · f · N · Φ_max
Where: – E = RMS induced voltage per phase – f = system frequency (Hz) – N = number of turns – Φ_max = maximum magnetic flux in the core (Wb)
In a delta–star transformer: – Delta side line voltage equals phase voltage – star side line voltage is √3 times the phase voltage
This directly affects turns ratio design:
V_L(Y) / V_L(Δ) = √3 · (N_Y / N_Δ)
2. Magnetic Flux Balance Under Unbalanced Loads
In three-phase transformers, the instantaneous sum of phase fluxes must satisfy:
Φ_A + Φ_B + Φ_C = 0
In delta-connected windings, zero-sequence currents (I₀) are allowed to circulate:
I₀ = (I_A + I_B + I_C) / 3
These circulating currents generate a compensating magnetomotive force (MMF):
MMF₀ = N · I₀
This internal MMF prevents zero-sequence flux from penetrating the core, maintaining flux symmetry and avoiding localized saturation.
Zero-Sequence Current and Grounding Theory
1. Symmetrical Components Perspective
According to symmetrical component theory:
[I_A I_B I_C]ᵀ = [1 1 1; 1 a² a; 1 a a²] · [I₀ I₁ I₂]ᵀ
Where: – I₀ = zero-sequence current – I₁ = positive-sequence current – I₂ = negative-sequence current – a = e^(j120°)
In a delta winding, zero-sequence currents form a closed loop and do not propagate upstream, effectively isolating the primary grid from downstream ground faults.
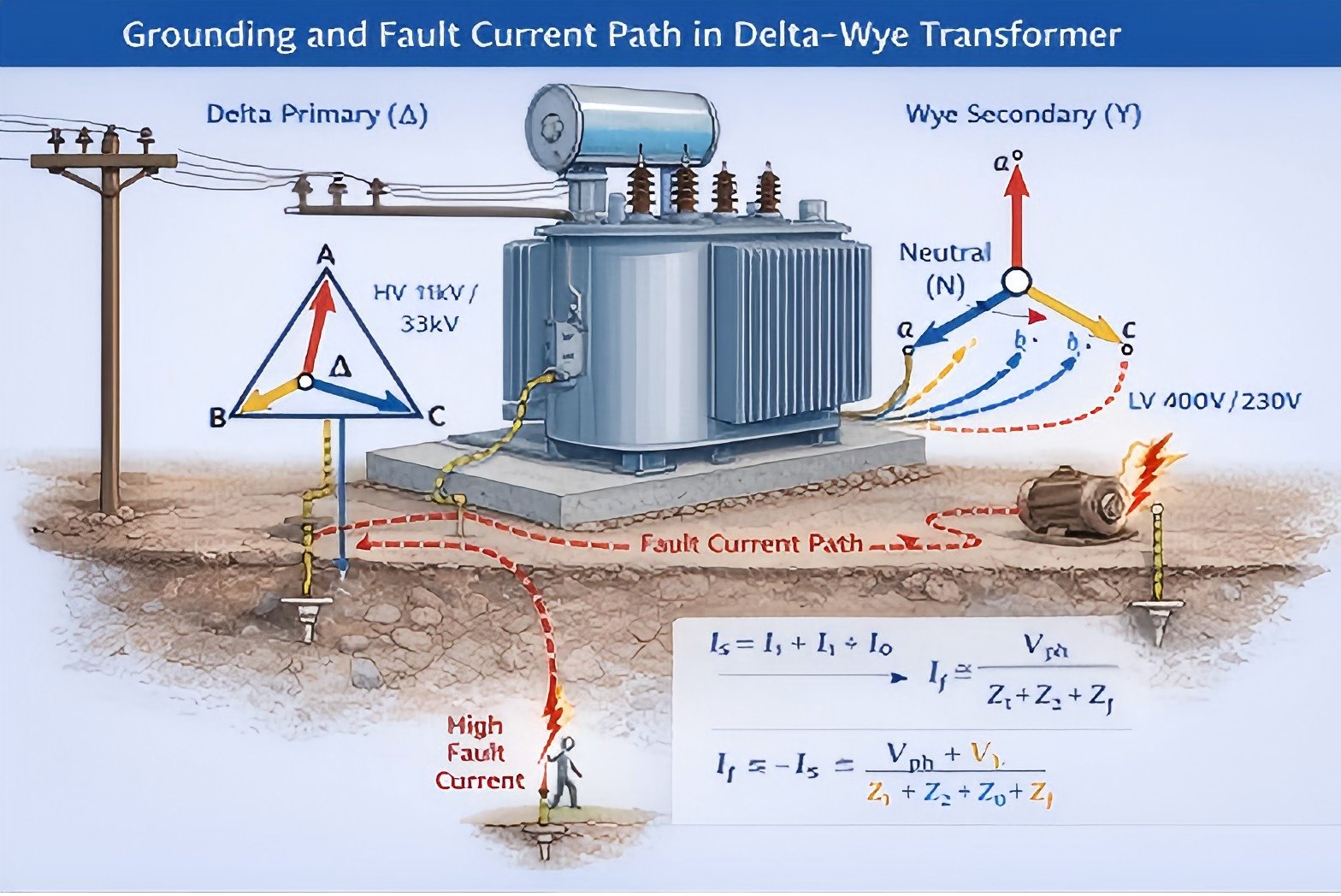
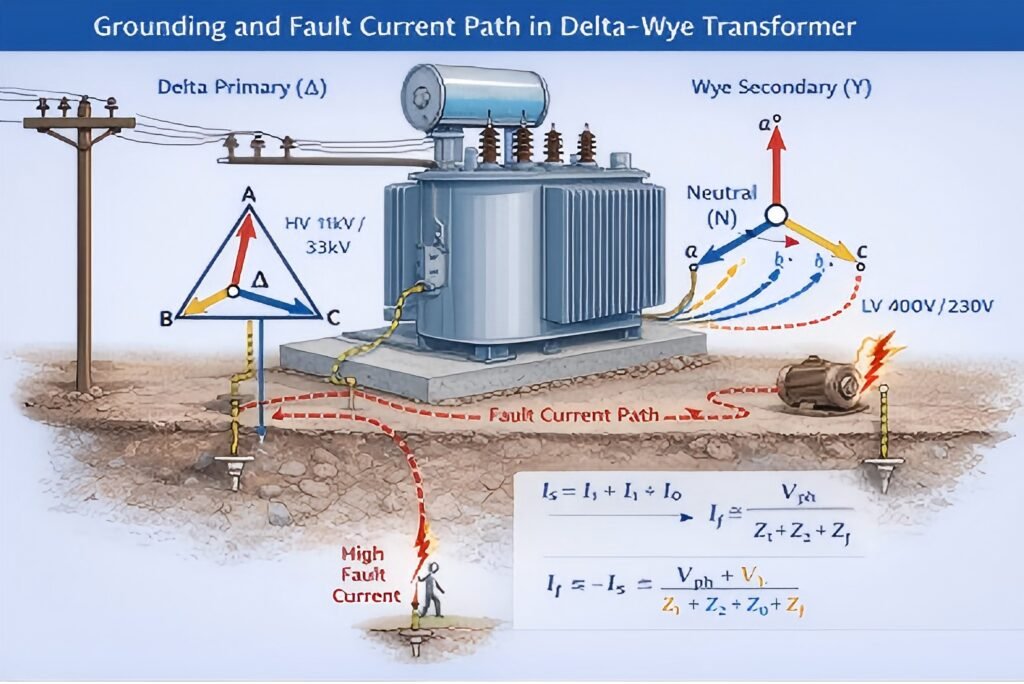
2. Ground Fault Current Path in Delta star Transformer
On the star-connected secondary with grounded neutral:
I_f = V_ph / (Z₁ + Z₂ + Z₀ + Z_f)
Where: – Z₁, Z₂, Z₀ = positive-, negative-, and zero-sequence impedances – Z_f = fault impedance
The presence of a grounded neutral ensures: – Stable fault current magnitude – Reliable relay operation – Accurate earth-fault detection
Harmonic Suppression Mechanism
1. Origin of Triplen Harmonics
Transformer magnetizing current is nonlinear due to the B–H characteristic of core steel:
B = μH + kH³ + …
This non linearity generates odd harmonics, particularly triplen harmonics (3rd, 9th, 15th), which are zero-sequence in nature.
2. Delta Loop Harmonic Circulation
In delta-connected winding:
I_3h(loop) = E_3h / Z_Δ
Triplen harmonic currents circulate inside the delta loop, rather than entering the supply system.
This results in: – Reduced voltage distortion – Lower neutral conductor heating – Improved compliance with IEEE 519 and IEC 61000
Comparison with Other Transformer Connections (Electromagnetic View)
Delta–star vs star–star (Y–Y)
In Y–Y transformers without tertiary delta:
- Zero-sequence current path is absent
- Zero-sequence flux must return through air and tank walls
Magnetically:
Φ₀ ∝ I₀ / ℜ_air
Where ℜ_air is high magnetic reluctance, causing: – Core saturation – Overheating – Voltage instability
Delta–star vs Delta–Delta (Δ–Δ)
Both configurations provide a delta loop for harmonics, but:
- Δ–Δ lacks a neutral point
- Single-phase load support is limited
- Ground protection schemes are complex
Thus, Δ–Y is more suitable for modern LV distribution.
Delta–star vs star–Delta (Y–Δ)
Y–Δ transformers are often used for step-up generation, where neutral grounding is not required on the secondary side. However:
- LV distribution requires phase-to-neutral loads
- Protection coordination is weaker
Hence, Y–Δ is rarely used for downstream distribution.
Design Trade-Offs and Engineering Constraints
While the delta–star connection transformer offers strong electromagnetic advantages, designers must consider:
- 30° phase shift preventing parallel operation with non-matching vector groups
- Higher insulation stress on star phase windings
- Increased complexity in protection coordination
Parallel operation condition:
Z_pu1 = Z_pu2 and Vector Group₁ = Vector Group₂
Typical Engineering Applications
- Utility distribution substations (33/11 kV, 11/0.4 kV)
- Industrial facilities with mixed nonlinear loads
- Data centers and commercial buildings
- Renewable energy LV interconnection points
Conclusion
From the standpoint of electromagnetic field theory, symmetrical components, and harmonic analysis, the delta star connection transformer represents an optimized solution for real-world power systems. Its ability to maintain magnetic flux balance, suppress zero-sequence harmonics, and provide a grounded neutral makes it technically superior to many alternative configurations.
For overseas EPC projects and utility-grade applications, selecting a delta star transformer is not only an industry norm—but a decision firmly grounded in electromagnetic science.
Author: QIANLAI –Transformer Manufacturer & Exporter | Specialized in IEC / IEEE Compliant Distribution and Power Transformers